特殊情况的二分算法。

每天一题 LeetCode81 Search in Rotated Sorted Array II

1. 题目

https://leetcode.com/problems/search-in-rotated-sorted-array-ii/

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3Output: falseFollow up:

• This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
• Would this affect the run-time complexity? How and why?

2. 解法

使用二分法，mid的位置有三种情况（google绘图，很丑，大概懂意思就行）：

图示	指针大小情况
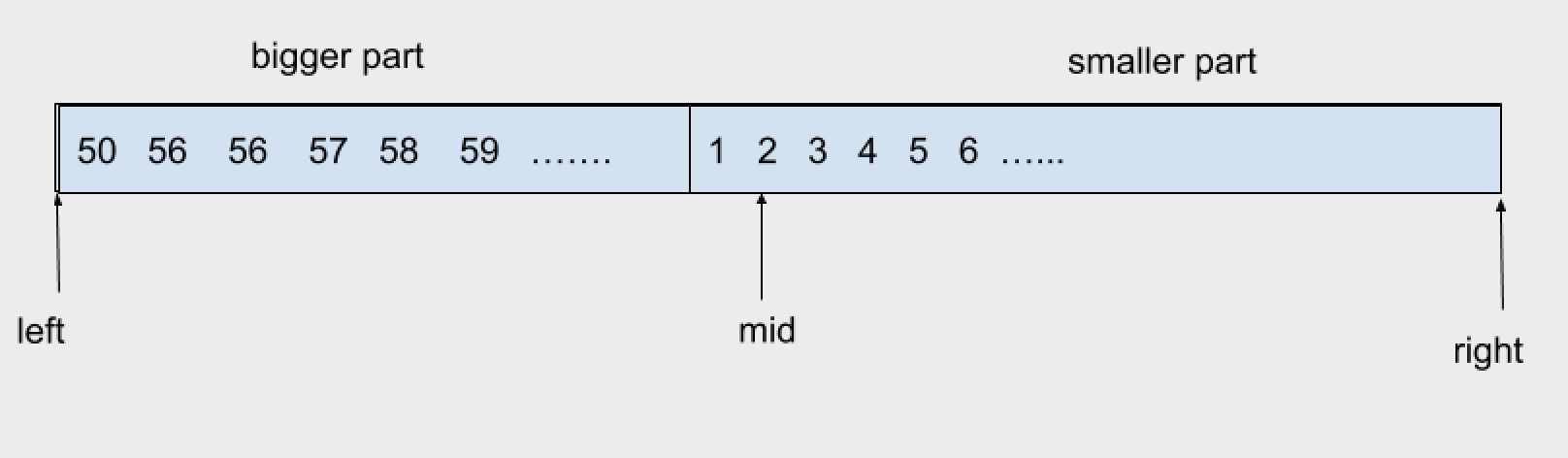	nums[mid] <= nums[right] <= nums[left]
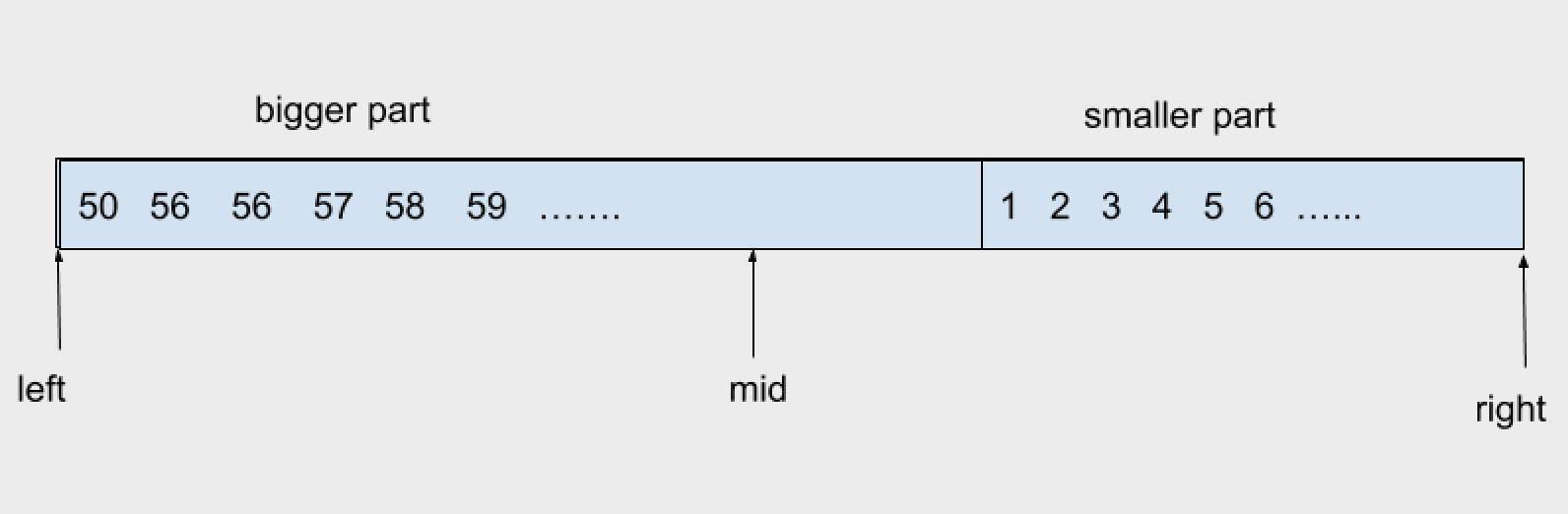	nums[right] <= nums[left] <= nums[mid]
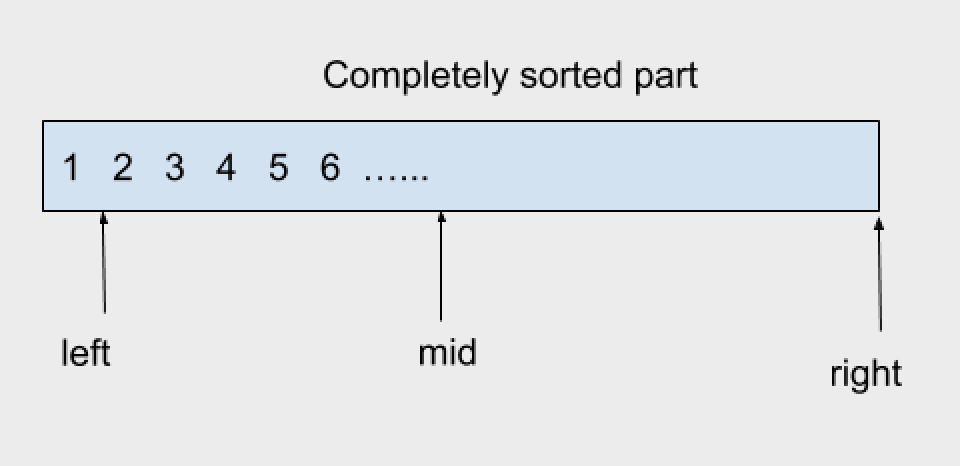	nums[left] <= nums[mid] <= nums[right]

再分别在这三种情况里针对target的位置进行判定就行了。
代码：

import "fmt"

func search(nums []int, target int) bool {
    l, r := 0, len(nums) - 1
    for l <= r {
        for l < r && nums[l+1] == nums[l]{ // 去重
            l++
        }
        for r > l && nums[r-1] == nums[r]{ // 去重
            r--
        }
        m := l + (r - l) / 2
        fmt.Println(l,m,r)
        switch{
        case nums[m] == target :
            return true 
        case nums[m] <= nums[r] && nums[r] <= nums[l]: //mid 在更小的这边
            if target < nums[m] || target > nums[r]{
                r = m - 1
            }else{
                l = m + 1
            }
        case nums[r] <= nums[l] && nums[l] <= nums[m]: //mid 在更大的这边
            if target < nums[m] && target > nums[r]{
                r = m - 1
            }else{
                l = m + 1
            }
        case nums[l] <= nums[m] && nums[m] <= nums[r]: //l与r之间是顺序
            if target < nums[m]{
                r = m - 1
            }else{
                l = m + 1
            }
        }
    }
    return false
}